

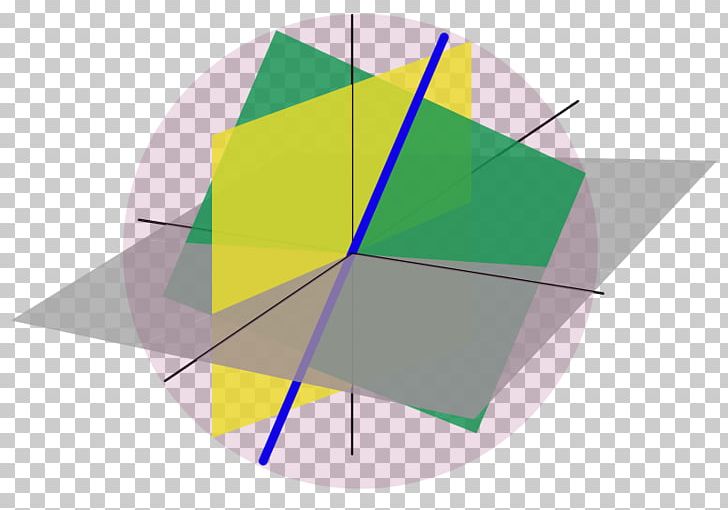
Of course, in either description, this is a plane. 5.3 VECTOR SUBSPACE Sometimes the entire region of a vector space may not be of. It must be closed under addition: if v1S v 1 S and v2S v 2 S for any v1,v2 v 1, v 2, then it must be. Mocanu proves thatĬ ∞ cannot be a Banach algebra under its usual topology. Now the subspace is described as the collection of unrestricted linear combinations of those two vectors. Subspaces It must contain the zero-vector. 2.1 Definition For any vector space, a subspace is a subset that is itself a. Carpender since 1971, shown without the property Q. understanding, keyed on the Linear Combination Lemma, of how it finds the. As a direct corollary he takes the uniqueness of the topology in commutative semisimple Fréchet Q–algebras, a known result due to R.L. Any subspace of a vector space other than itself is. Aupetit related to the uniqueness of the complete norm in semisimple Banach algebras (see beginning of Section 2), in the context of commutative m *–convex Q–algebras (see ). Let V be a real vector space (e.g., the real continuous functions C(I) on a closed interval I, two-dimensional Euclidean space R2, the twice differentiable. A subset of a vector space is a subspace of if is a vector space itself under the same operations. This follows from a more general result according to which the cartesian product of infinitely many normed spaces, cannot be a normed space under the product topology. ( A λ ) λ ∈ Λ of Banach algebras, under the product topology (see Example 7.6(2)). Let V be a vector space and let S be a subset of V such that S is a vector space with the same + and from V. (1) Another example of an Arens–Michael algebra that cannot be topologized as a Banach algebra, is the cartesian product Hence, x ∈ J implies yx ∈ J, for every y ∈ A. From Theorem 4.6(4), (7) and (8) one has that J is an ideal. In fact, the column space and nullspace are intricately connected by the rank-nullity theorem, which in turn is part of the fundamental theorem of linear algebra.A subset of a vector space is a subspace if it is a vector space itself under the same operations.

(Definitions of orthogonality for other spaces are perfectly possible, but we haven't seen any in this book. This definition doesn't involve a sense of 'orthogonal' so we can apply it to spaces other than subspaces of an. This establishes that the nullspace is a vector space as well. For any direct sum and any, the projection of onto along is. For instance, consider the set W W W of complex vectors v \mathbf \in N c v ∈ N for any scalar c c c. The simplest way to generate a subspace is to restrict a given vector space by some rule. A subspace is said to be invariant under a linear operator if its elements are transformed by the linear operator into elements belonging to the subspace itself.


 0 kommentar(er)
0 kommentar(er)
